Experimental Mathematics Website
http://www.experimentalmath.info
|
|
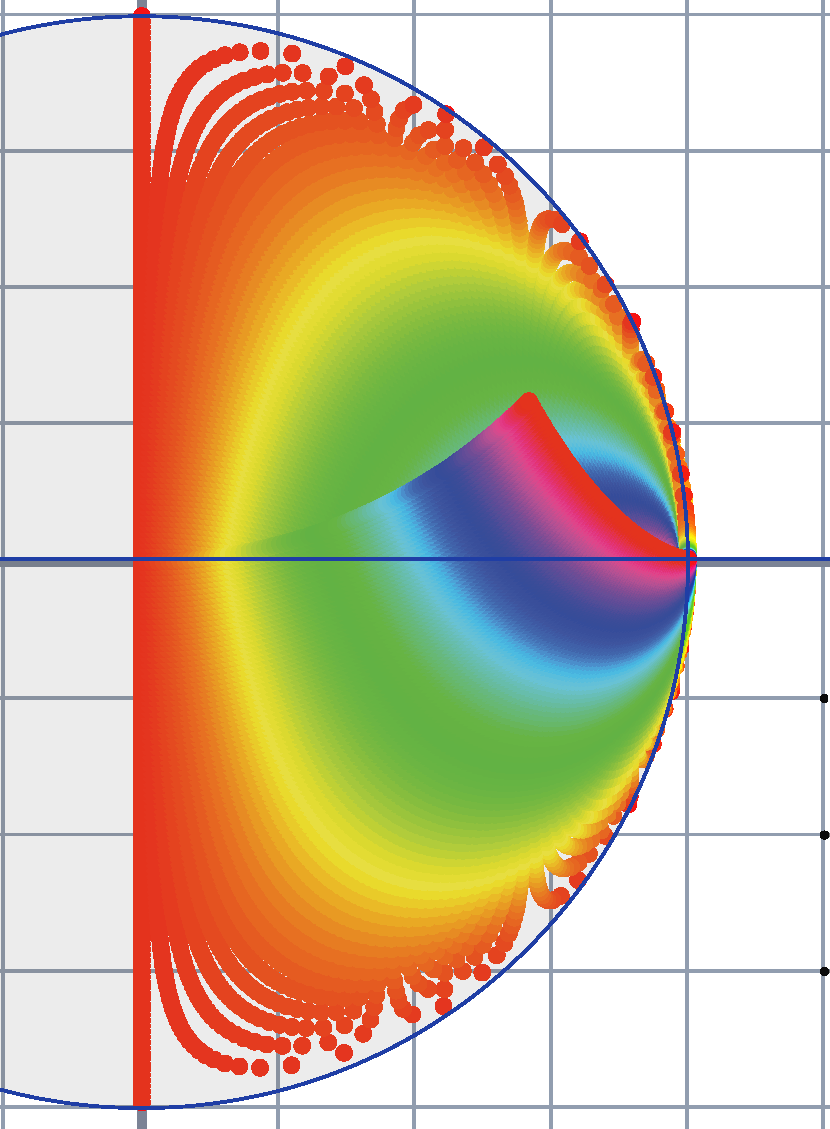
<== This is a picture from the interactive geometry
package Cinderella showing the behavior of 10,000 starting
values in the rectangle [0,1]x[h-1,h+1], where h is the height of the
horizontal line, after six iterations of the algorithm which reflects
a point x in the sphere then reflects the outcome in the line and then
averages the result y with x. It is an accessible prototype for a
remarkable image reconstruction algorithm known variously as
Douglas-Ratchford, Lion-Mercier, Fienup's method, and
"divide-and-concur." Some related graphics can be generated and
displayed at these URLs:
Expansion
Reflection
(wait 30-60 seconds to see the display).
Quote of the day (refresh browser to select another):
In 1831, Fourier's posthumous work on equations showed 33 figures of solution, got with enormous labour. Thinking this is a good opportunity to illustrate the superiority of the method of W. G. Horner, not yet known in France, and not much known in England, I proposed to one of my classes, in 1841, to beat Fourier on this point, as a Christmas exercise. I received several answers, agreeing with each other, to 50 places of decimals. In 1848, I repeated the proposal, requesting that 50 places might be exceeded: I obtained answers of 75, 65, 63, 58, 57, and 52 places. -- Augustus De Morgan, quoted from Adrian Rice, "The Case of Augustus De Morgan", American Mathematical Monthly, Jun-Jul 1999, pg. 542.
The complete list of quotes is available
here.
|
This website is a repository of information on experimental and computer-assisted mathematics. It is operated by David H. Bailey, Lawrence Berkeley Laboratory (retired), and University of California, Davis
(DHB website).
Please send any comments or questions for this site to:
Disclaimer and copyright. Material on this site is provided for research purposes only and does not necessarily reflect the views or policies of the author's institutions or any other organization. Except where explicitly stated otherwise, all material is copyrighted by David H. Bailey (c) 2024.
Math Scholar blog. The "Math Scholar" blog contains essays, philosophical musings, interesting quotes and exercises, all in the realm of mathematics, computing and modern science. New items are posted on average every two weeks:
Math Drudge blog (older). This blog was co-authored by Bailey and the late Jonathan Borwein, prior to Borwein's death in August 2016.
Jonathan Borwein Memorial site. In the wake of Jonathan Borwein's untimely death in August 2016, this site contains a blog of remembrances of Jon by family, friends and colleagues, together with a compendium of Jon's publications, talks and reviews of his work by others.
Mathematical Investor blog. The Mathematical Investor blog is devoted to financial mathematics and abuses of mathematics in the field:
Additional information, in alphabetical order:
- Books. Bailey and Jonathan Borwein (now deceased) have authored numerous books on mathematical and scientific computation. For details on the authors' books on experimental mathematics, see:
- Commercial sites. For a list of websites of numerous commercial firms that offer mathematical software and (free) online tools, see the Commercial site page:
- Institutional sites. For a list of websites of mathematical societies and journals in the general area of experimental and computational mathematics, see the Institutional site page:
- Non-commercial software and tools. For a list of websites of non-commercial organizations that offer mathematical software and (free) online tools, see the Non-commercial site page:
- Other sites of interest. For a list of numerous other websites with interesting and useful information relevant to mathematics in general and computational mathematics in particular, see the Other site page:
- Software. For some freely downloadable software for experimental math research, see the Software page: